Introduction to Trigonometry

What is Trigonometry?

Trigonometry is a branch of mathematics that studies the relationship between the angles and sides of a right-angled triangle. It is especially useful in measuring heights, distances, and angles in real-world contexts like construction, navigation, and astronomy.

Right-Angled Triangle and Its Sides In a right-angled triangle, one of the angles is exactly 90°. The three sides of the triangle are:

Side	Symbol	Description
Perpendicular	𝑝	The side opposite to the angle being considered (not the right angle)
Base	𝑏	The side adjacent to the angle being considered (not the hypotenuse)
Hypotenuse	ℎ	The side opposite the right angle; the longest side in a right triangle

In a right-angled triangle $P^2 + B^2 = H^2$

Figure 1: Perpendicular, Base and Hypotenuse in a triangle.

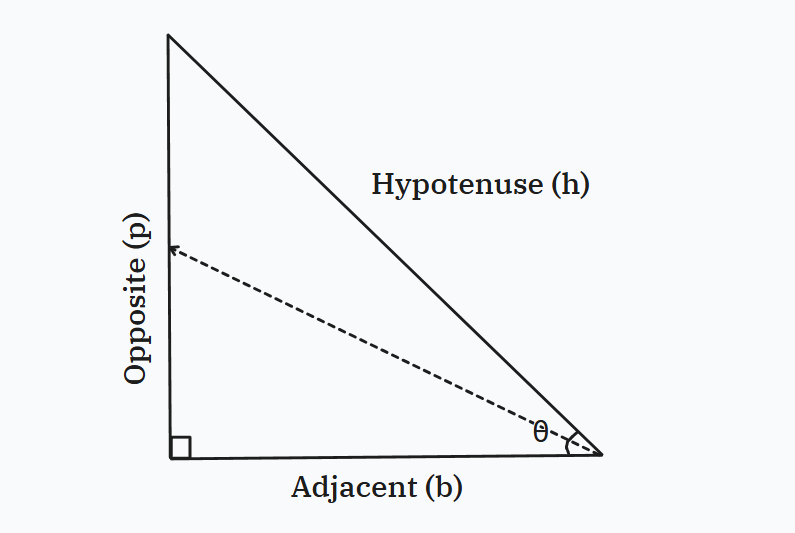
Figure 2: Relations of p, b and h with theta (θ)

Trigonometric Ratios

For a right-angled triangle with angle 𝜃, the basic trigonometric ratios are:

$\sin\theta = \dfrac{p}{h}$

$cos \theta = \dfrac{b}{h}$

$tan \theta = \dfrac{p}{b}$

📐 Trigonometric Ratios Table (Standard Angles)

$( \theta ) (Degrees)$	$( \sin \theta )$	$( \cos \theta )$	$( \tan \theta )$
$( 0^\circ )$	$( 0 )$	$( 1 )$	$( 0 )$
$( 30^\circ )$	$( \frac{1}{2} )$	$( \frac{\sqrt{3}}{2} )$	$( \frac{1}{\sqrt{3}} )$
$( 45^\circ )$	$( \frac{1}{\sqrt{2}} )$	$( \frac{1}{\sqrt{2}} )$	$( 1 )$
$( 60^\circ )$	$( \frac{\sqrt{3}}{2} )$	$( \frac{1}{2} )$	$( \sqrt{3} )$
$( 90^\circ )$	$( 1 )$	$( 0 )$	Not defined

📐 Trigonometric Ratios – Standard Angles

Ratio	$0^\circ$	$30^\circ$	$45^\circ$	$60^\circ$	$90^\circ$
$\sin \theta$	$0$	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$	$1$
$\cos \theta$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$	$0$
$\tan \theta$	$0$	$\frac{1}{\sqrt{3}}$	$1$	$\sqrt{3}$	Not defined