Operations on Sets
Set operations help us combine, compare, or separate sets based on their elements. These operations are useful in organizing data, solving problems, and understanding relationships between groups.
Common Set Operations
- Union (A ∪ B): All elements in A or B or both.
- Intersection (A ∩ B): Elements common to A and B.
- Difference (A − B): Elements in A not in B.
- Complement (Aᶜ): Elements not in A (relative to universal set U).
1. Union of Sets (A ∪ B)
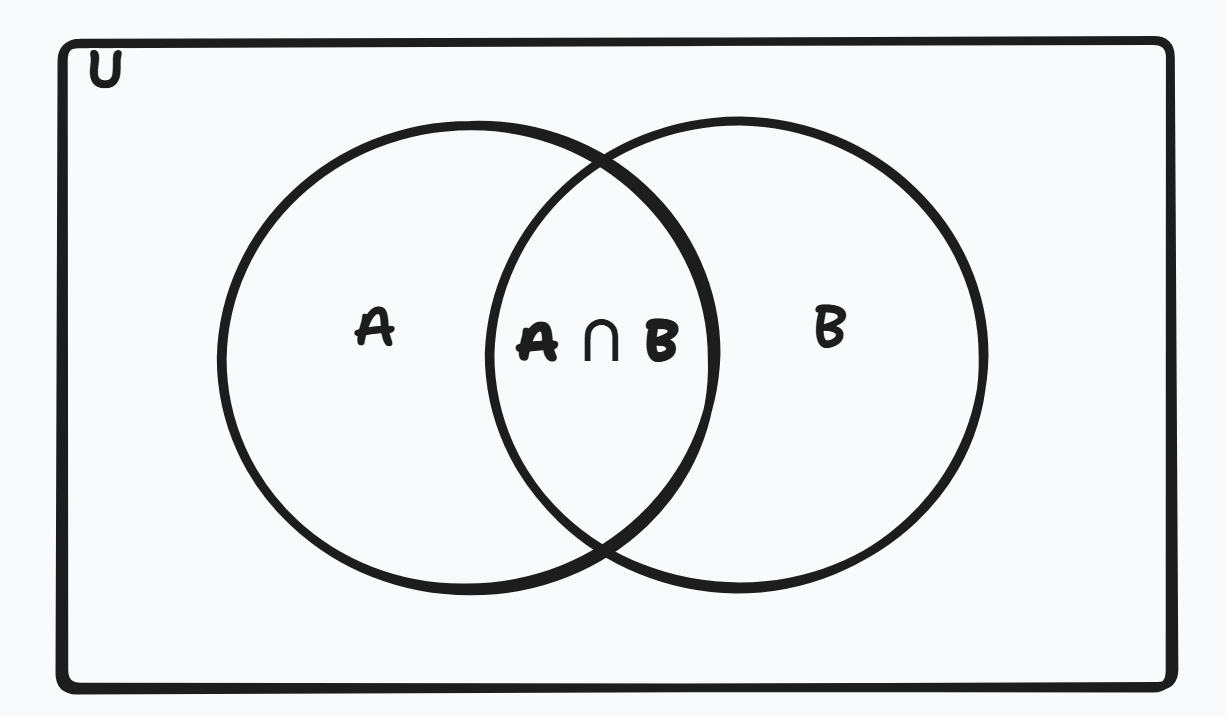
Figure 1: Union of two sets A and B.
The union of two sets A and B includes all elements that are in A, in B, or in both.
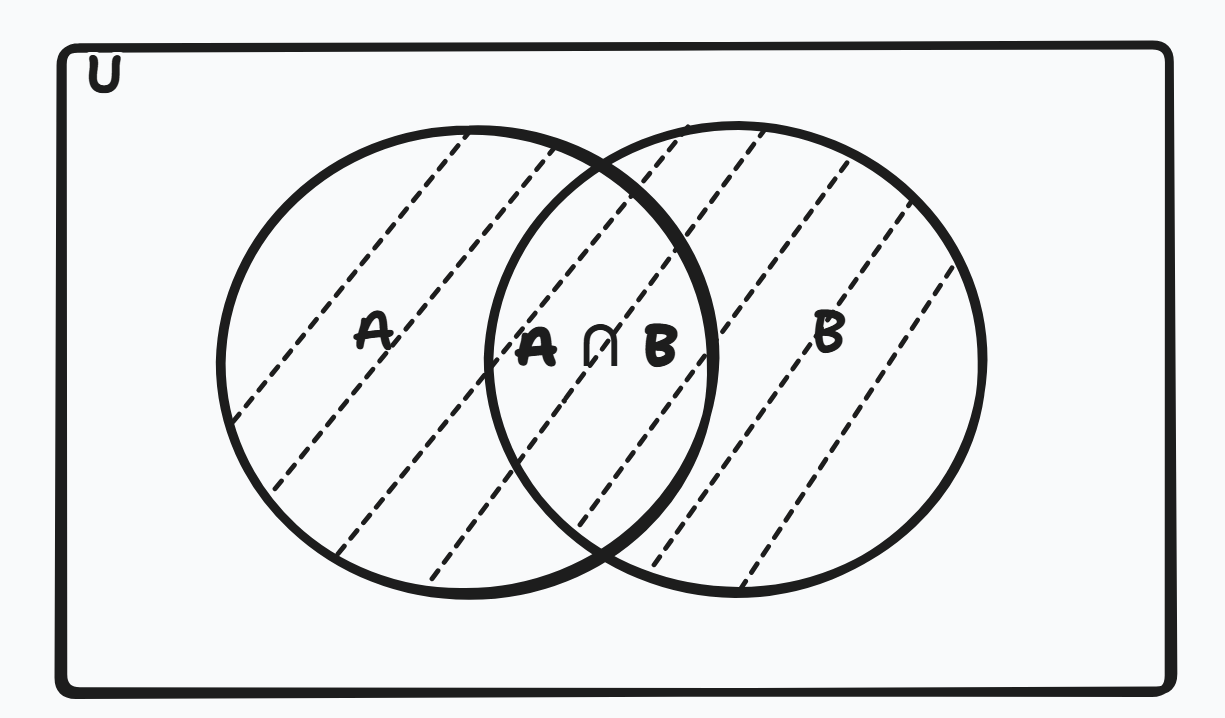
Figure 2: Union of two sets A and B (shaded).
Duplicate elements are written only once.
Example: If A = {1, 2, 3, 4, 5, 6} B = {4, 5, 6, 7} Then A ∪ B = {1, 2, 3, 4, 5, 6, 7}
Set Builder Notation: A ∪ B = {x : x ∈ A or x ∈ B}
2. Intersection of Sets (A ∩ B)
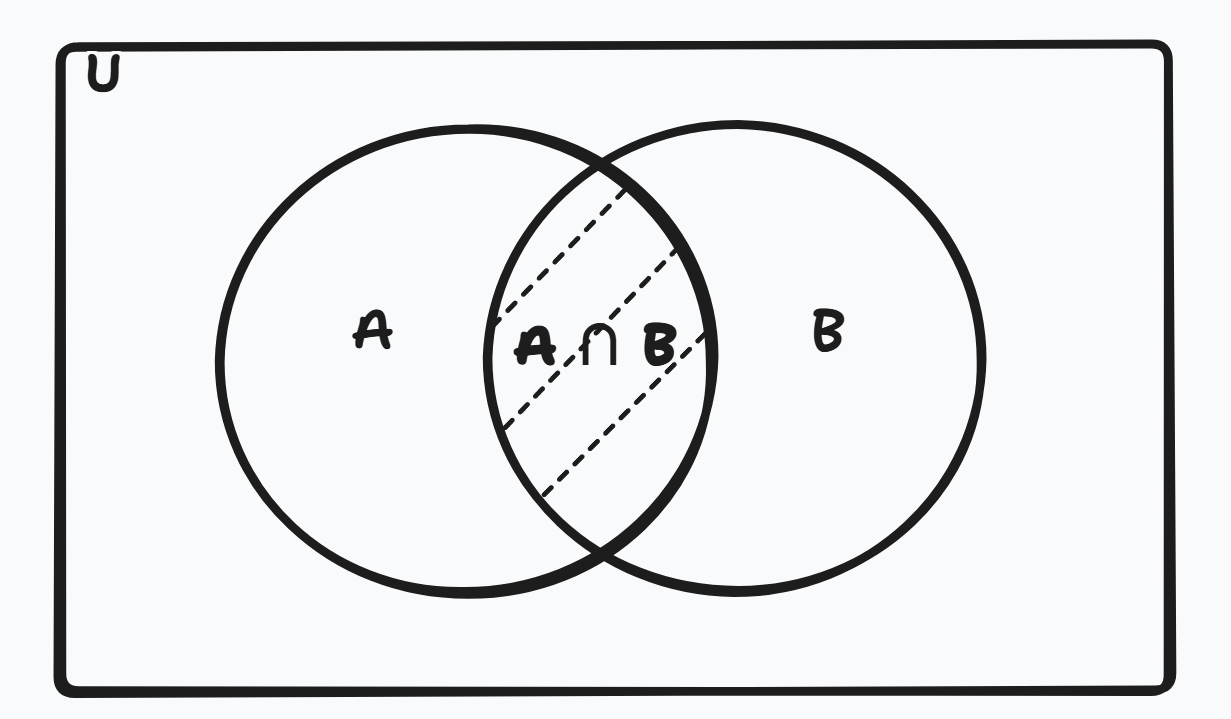
Figure 3: Intersection of two sets A and B.
The intersection includes only the elements that are common to both sets A and B.
Example: A = {1, 2, 3, 4, 5, 6} B = {4, 5, 6, 7} Then A ∩ B = {4, 5, 6}
Set Builder Notation: A ∩ B = {x : x ∈ A and x ∈ B}
3. Difference of Sets (A − B)
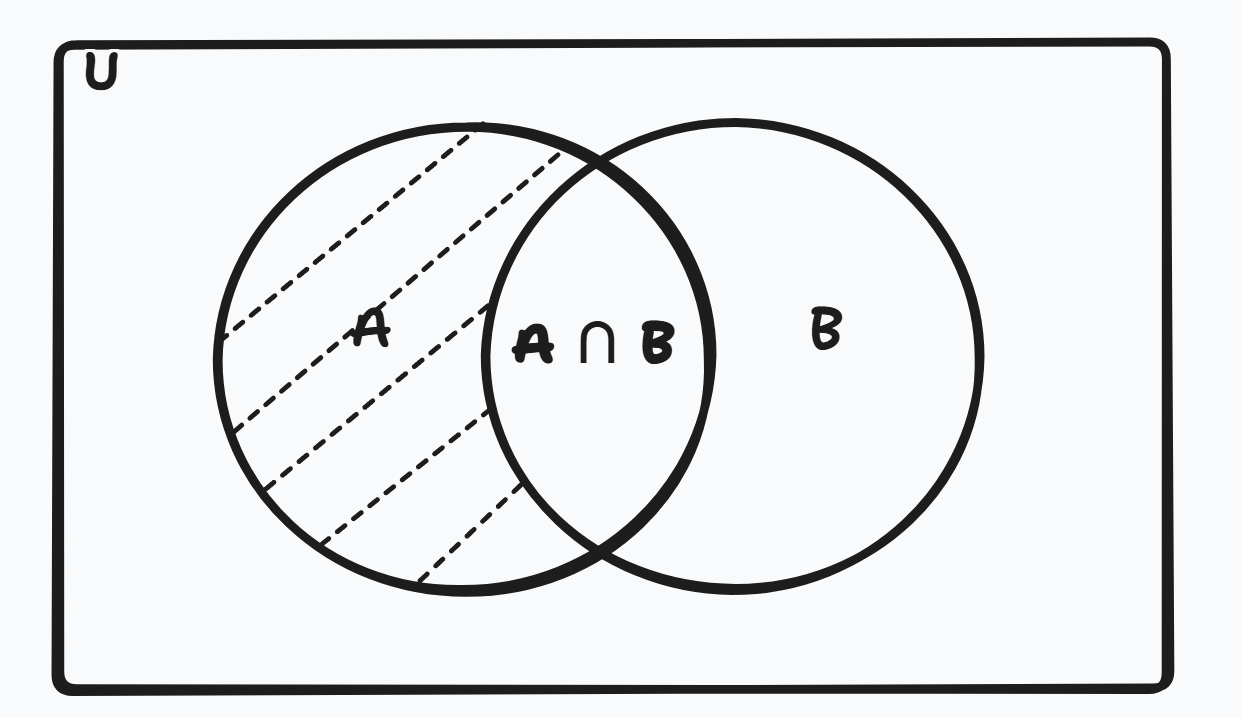
Figure 4: Set Difference: (A - B).
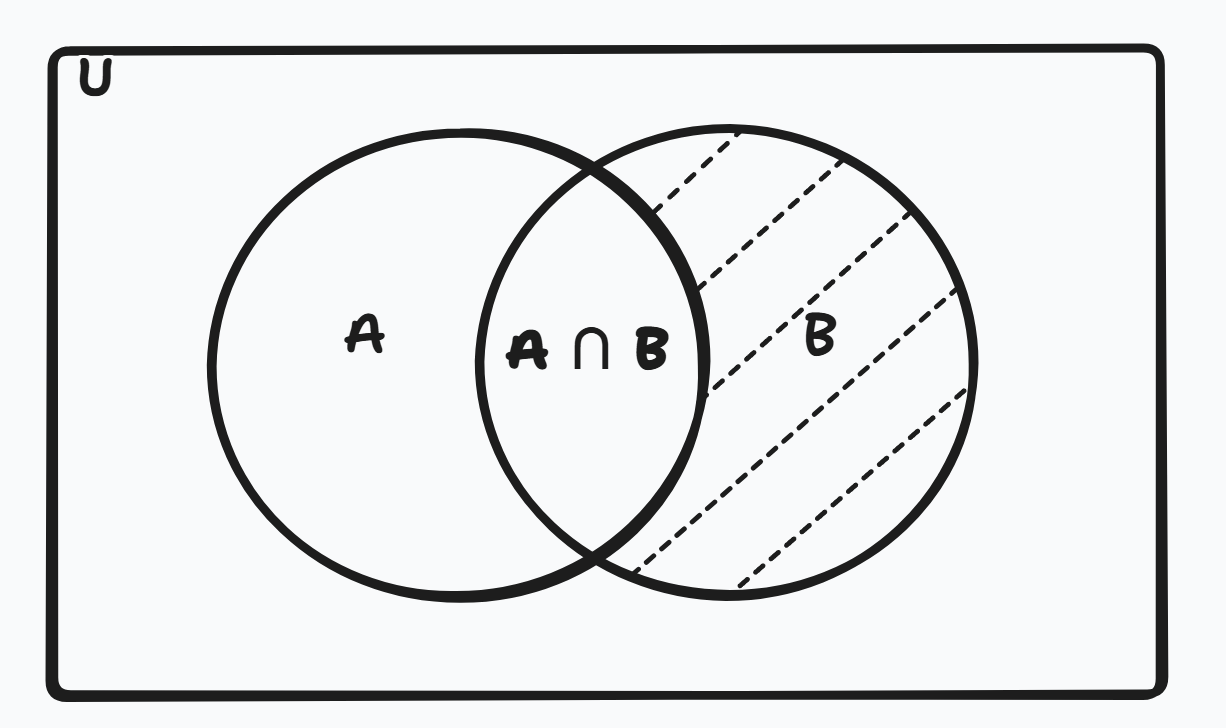
Figure 5: Set Difference: (B - A).
The difference A − B includes elements that are in A but not in B.
Example: A = {1, 2, 3, 4, 5, 6} B = {4, 5, 6, 7} Then A − B = {1, 2, 3}
Note: A − B = A − (A ∩ B)
Remember that A ∩ B = B ∩ A, but A − B ≠ B − A.
4. Symmetric Difference (A Δ B)

Figure 6: Symmetric Difference: (A Δ B).
The symmetric difference includes elements that are in A or B but not in both.
Formula: A Δ B = (A − B) ∪ (B − A)
Example: A − B = {1, 2, 3} B − A = {7} So, A Δ B = {1, 2, 3, 7}
5. Complement of a Set [A̅ or (A∪B)c]
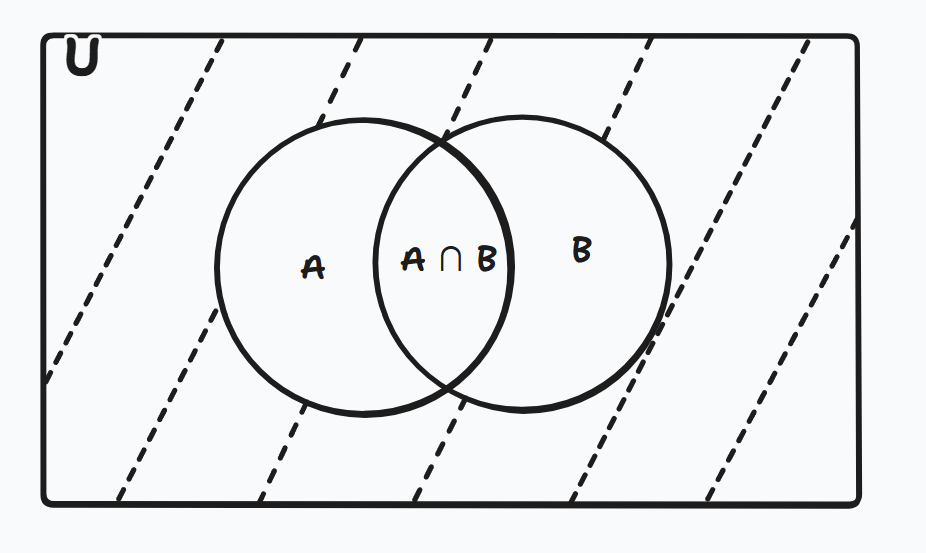
Figure 7: Complement of A union B: (A ∪ B)c.
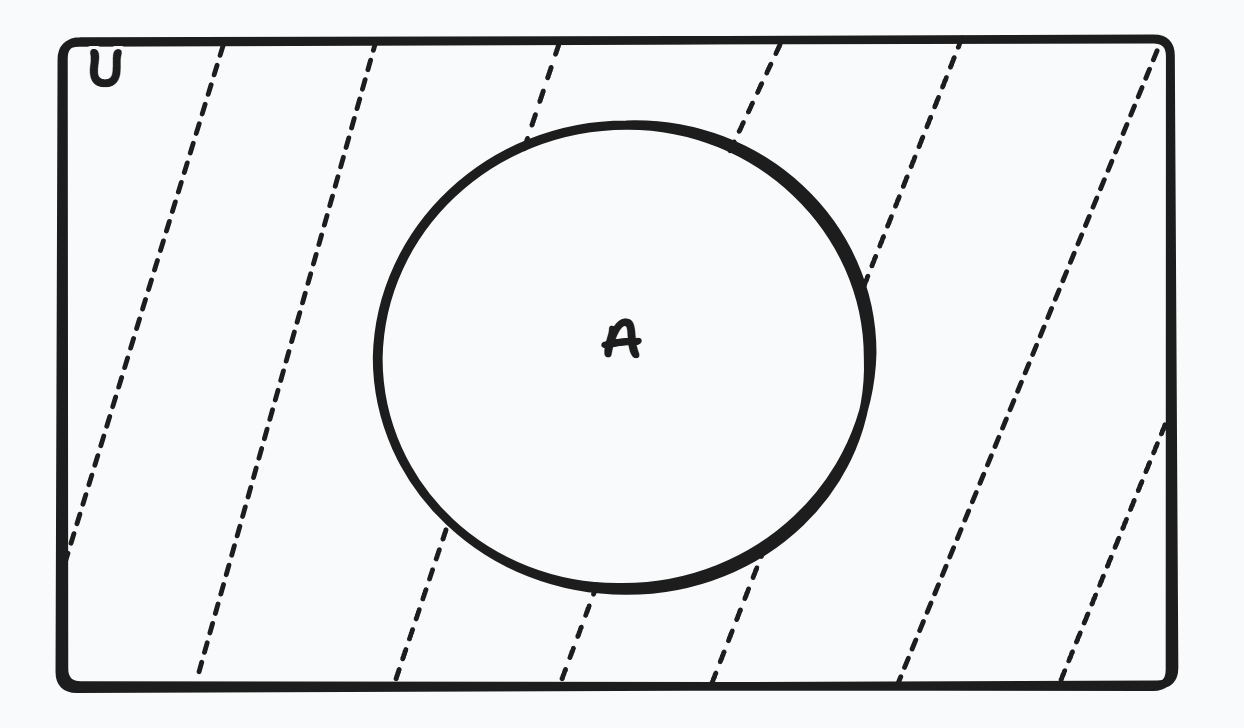
Figure 8: Complement of A: (A̅) or A c .
The complement of set A includes all elements in the universal set U that are not in A.
Example: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} A = {1, 3, 5, 7, 9} Then A̅ = {2, 4, 6, 8, 10}
Set Builder Notation: A̅ = {x : x ∈ U and x ∉ A}