Introduction to Sets

A set is a well-defined collection of distinct objects. Well-defined means we can clearly decide whether an object belongs to the set or not.

Examples include:

• Set of prime numbers less than 10: {2, 3, 5, 7}
• Set of letters in the word "NEPAL": {N, E, P, A, L}
• Natural numbers: N = {1,2,3,...}

We will study operations on sets, cardinality, exercises, and quizzes in this unit.

Examples from Daily Life

Real-world Group	Set Representation
Students in a football team	F = {Hari, Shyam, Ram, Jivan, Priyanka}
Students in a basketball team	B = {Ivan, Bella, Sameer, Jivan}
Days of the week	D = {Sunday, Monday, Tuesday, ..., Saturday}
Vowels in English	V = {a, e, i, o, u}

Key Terms

Term	Meaning
Element	An individual object in a set
Set	A group of well-defined elements
Subset	A set whose elements are all contained in another set
Universal	Set The set that contains all elements under discussion
Venn Diagram	A visual way to show sets and their relationships using closed shapes

Subsets

A subset is a set whose elements are all contained within another set. If every element of set $A$ is also in set $B$, then $A$ is a subset of $B$ (written as $A \subseteq B$).

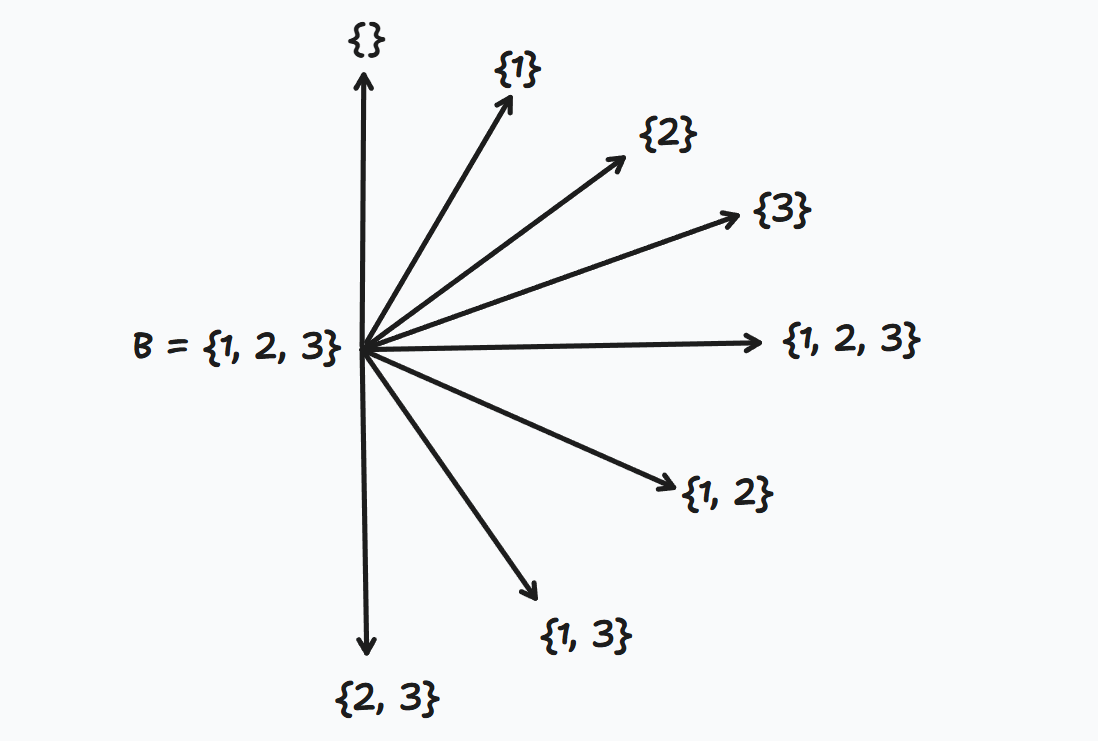
Example: Let $B = \{1, 2, 3\}$

Possible subsets of $B$ include:

• $\{\}$ (the empty set)

• $\{1\}$, $\{2\}$, $\{3\}$

• $\{1, 2\}$, $\{2, 3\}$, $\{1, 3\}$

• $\{1, 2, 3\}$

Figure 1: Subsets of: B = {1, 2, 3}.

Types of Subsets

1. Proper Subset

A proper subset of $B$ is a subset that is not equal to $B$ itself.
Notation: $A \subset B$

Example:
$\{1, 2\}$ is a proper subset of $\{1, 2, 3\}$.

2. Improper Subset

An improper subset is the set itself.
$\{1, 2, 3\}$ is an improper subset of $\{1, 2, 3\}$.

3. Empty Set (Null Subset)

The empty set ($\{\}$) is a subset of every set.

Counting Subsets

If a set has $n$ elements, the total number of subsets is $2^n$ (including the empty set and the set itself).

Example:
For $B = \{1, 2, 3\}$ ($n = 3$):

• Total subsets: $2^3 = 8$

List of all subsets:

• $\{\}$
• $\{1\}$
• $\{2\}$
• $\{3\}$
• $\{1, 2\}$
• $\{1, 3\}$
• $\{2, 3\}$
• $\{1, 2, 3\}$

Proper subsets exclude the set itself: $2^n - 1$
For $B$, proper subsets: $8 - 1 = 7$

Disjoint Sets

Two sets are disjoint if they have no elements in common.
Formally, sets $A$ and $B$ are disjoint if $A \cap B = \emptyset$ or $\{ \}$.

Impact on Set Operations

• Intersection: For disjoint sets, $A \cap B = \emptyset$.
• Union: The union simply combines all elements: $A \cup B$ contains all elements from both sets.
• Cardinality: If $A$ and $B$ are disjoint, $n(A \cup B) = n(A) + n(B)$.

Real-world Examples

Scenario	Set $A$	Set $B$	Disjoint?
Boys and girls in a class	$\{$Ravi, Sam$\}$	$\{$Priya, Sita$\}$	Yes
Prime numbers and even numbers	$\{$2, 3, 5, 7$\}$	$\{$2, 4, 6, 8$\}$	No
Students in football vs chess	$\{$Ivan, Bella$\}$	$\{$Samir, Pratyusha$\}$	Yes

NOTE

$2$ is both prime and even, so these sets are not disjoint.

Formula

If $A$ and $B$ are disjoint:

$$n(A \cup B) = n(A) + n(B)$$

If not disjoint:

$$n(A \cup B) = n(A) + n(B) - n(A \cap B)$$

Disjoint sets are important in probability, counting, and organizing groups with no overlap.