Introduction to Geometry

---

Triangle

---

Definition

A triangle is a closed figure formed by three line segments. It has:

• 3 sides

• 3 angles

• 3 vertices

---

Properties of a Triangle

1. Angle Sum Property:

   The sum of interior angles of any triangle is always:
   $\angle A + \angle B + \angle C = 180^\circ$

   

   Figure 1: Triangle with sides and angles.

2. Exterior Angle Property:

   An exterior angle is equal to the sum of the two opposite interior angles:
   $\angle D = \angle A + \angle B$

   

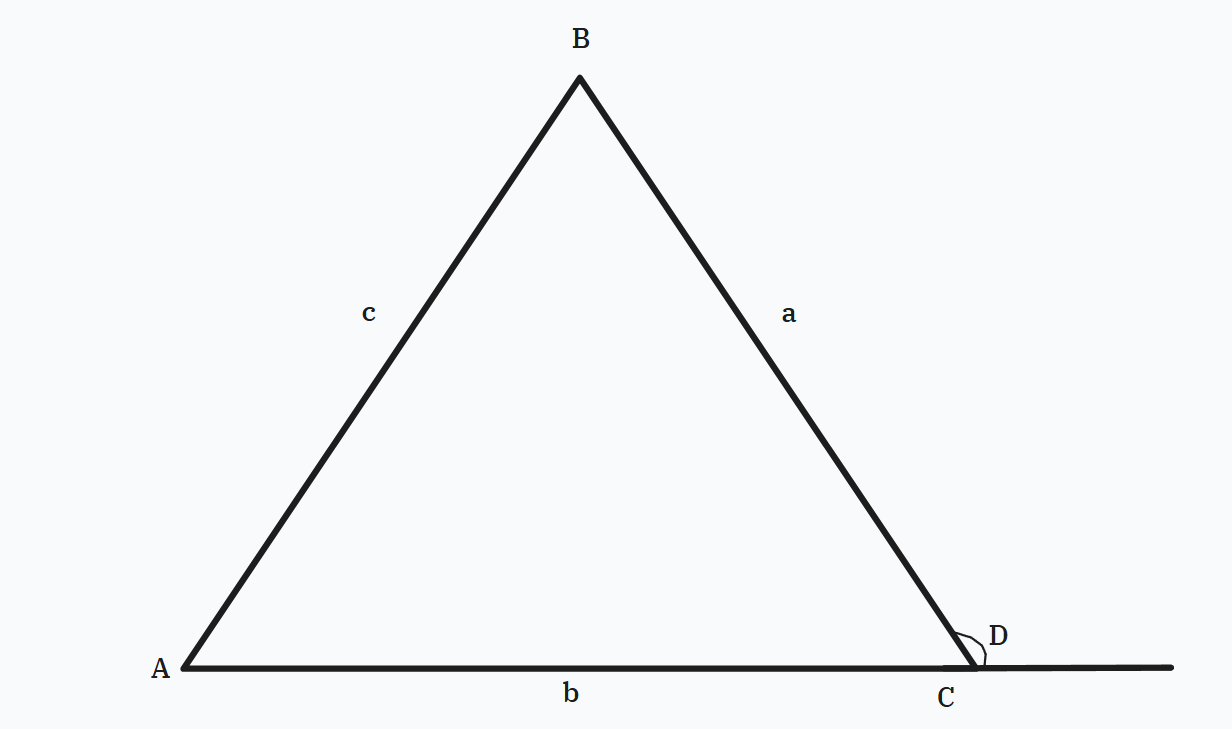
   Figure 2: Triangle with angles (A, B, C) and exterior angle D.

3. Triangle Inequality Theorem:

   The sum of any two sides is greater than the third side:
   $a + b > c$,

   $b + c > a$,

   $c + a > b$

4. Area of Triangle (basic):

   $\text{Area} = \dfrac{1}{2} \cdot \text{base} \cdot \text{height}$

   In Figure(2), base = AC, and height = BD

   

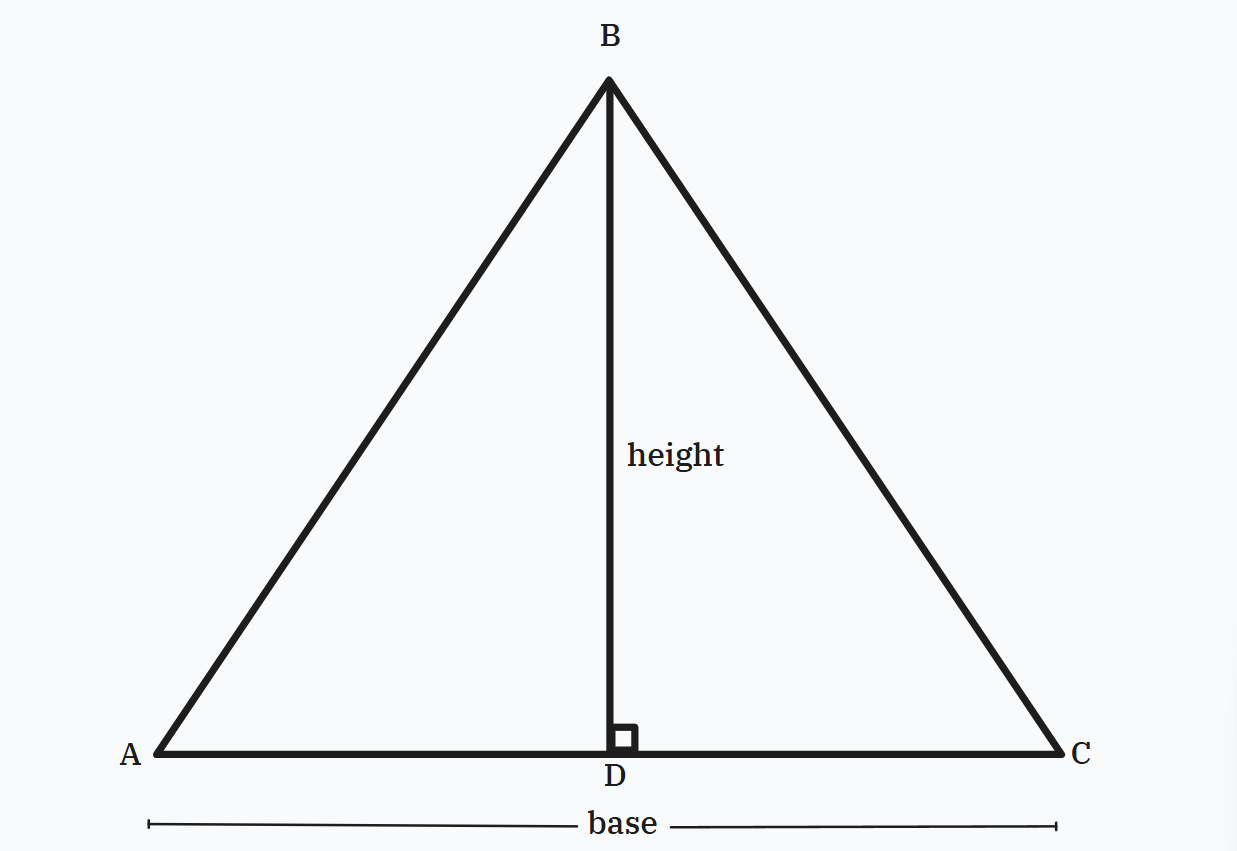
   Figure 3: Triangle with Base (AC), and height (BD).

   Base and Height

   Base $\perp$ Height: Any side can be taken as base, but the Height is perpendicular to the base and touches the opposite vertex.

---

Types of Triangles

By Sides:

• Scalene Triangle: All three sides and all three angles are different.

  • Sides: a, b, c (all distinct)

  • Perimeter: $P = a + b + c$

  • Area (Heron’s formula): let $s = \dfrac{a+b+c}{2}$, then $\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}$

• Isosceles Triangle: Two sides equal and the base angles equal.

  • Sides: equal sides $a, a$ and base $b$

  • Base angles are equal; vertex angle is opposite the base.

  • Perimeter: $P = 2a + b$

  • Height from the apex to base: $h = \sqrt{a^2 - \dfrac{b^2}{4}}$

  • Area: $\text{Area} = \dfrac{1}{2} \, b \, h = \dfrac{b}{4}\sqrt{4a^2 - b^2}$

• Equilateral Triangle: All sides equal and all interior angles are $60^\circ$.

  • Side: $a$ (all three sides equal)

  • Angles: each $60^\circ$

  • Perimeter: $P = 3a$

  • Height: $h = \dfrac{\sqrt{3}}{2}\,a$

  • Area: $\text{Area} = \dfrac{\sqrt{3}}{4}\,a^2$

By Angles:

• Acute Triangle: All angles < $90^\circ$

• Right Triangle: One angle = $90^\circ$

• Obtuse Triangle: One angle > $90^\circ$

---

Relationship Among Sides and Angles

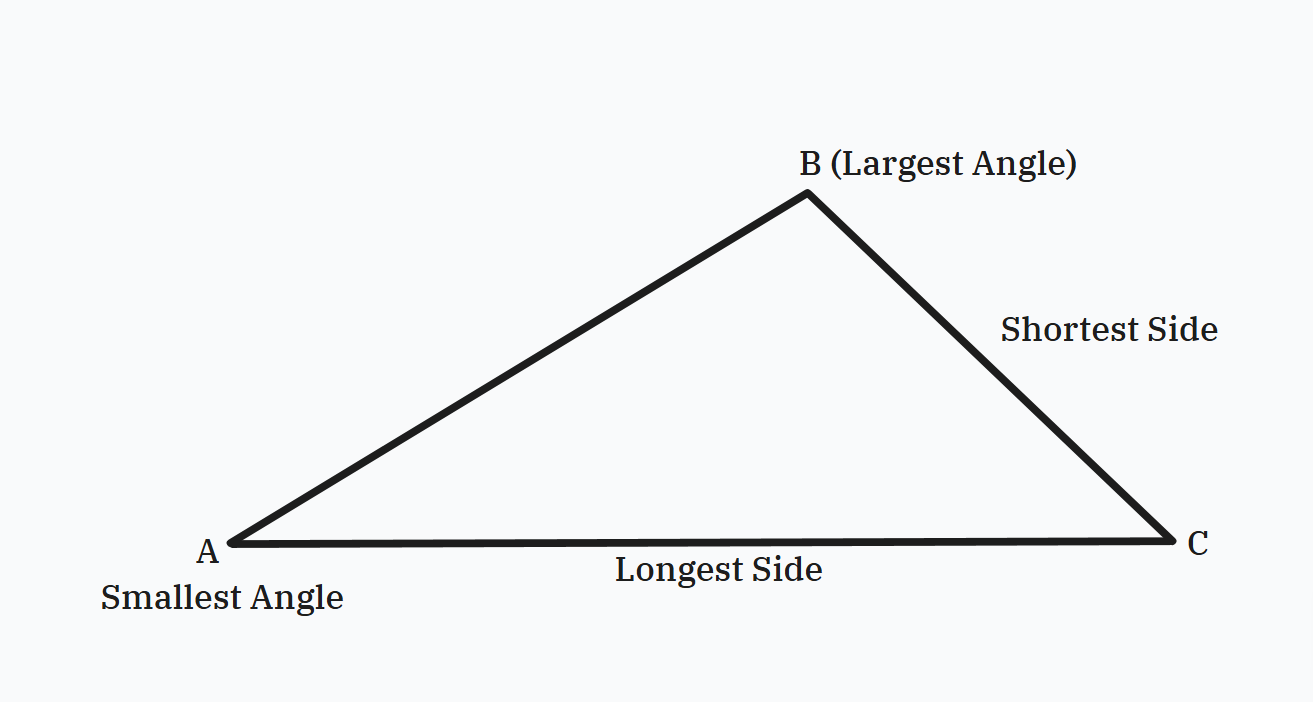
Figure 4: Triangle with variable length of sides.

• Longest side is opposite the largest angle

• Shortest side is opposite the smallest angle

Pythagoras Theorem (Right Triangle):

$P^2 + B^2 = H^2$

Where, $H$ is the hypotenuse,

$P$ is the Perpendicular ( Opposite ), and

$B$ is the Base ( Adjacent )

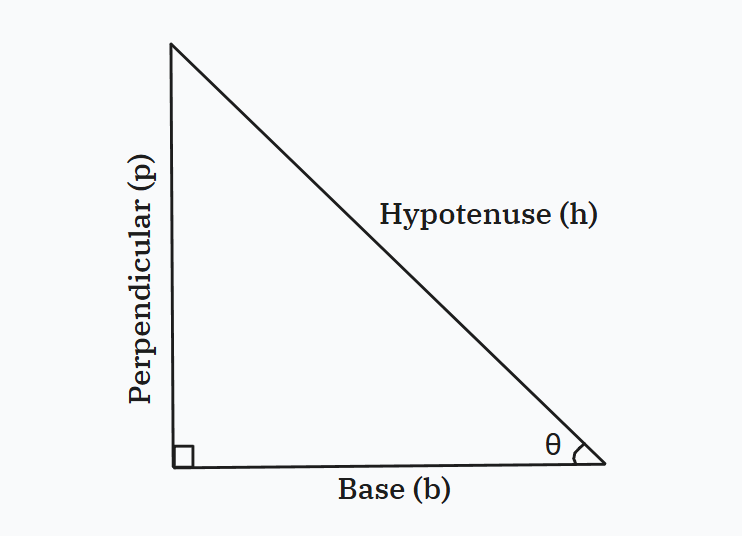
Figure 5: Right Angled Triangle.

---

Similar Triangles

Definition:

Two triangles are similar if:

• Their corresponding angles are equal

• Their corresponding sides are in the same ratio

Figure 6: Two similar triangles.

Symbol:

$\triangle ABC \sim \triangle DEF$

Conditions for Similarity:

1. AA (Angle-Angle): Two pairs of equal angles

2. SSS (Side-Side-Side): All sides in same ratio

3. SAS (Side-Angle-Side): Two sides in same ratio and included angle equal

Properties:

• Ratio of corresponding sides:

  $\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}$

• Ratio of areas:

  $\dfrac{\text{Area of } \triangle ABC}{\text{Area of } \triangle DEF} = \left( \dfrac{\text{side of } \triangle ABC}{\text{corresponding side of } \triangle DEF} \right)^2$

---

Real-World Applications

• Map scaling and model design

• Shadow length problems

• Architecture and trigonometry